不等辺三角形 高精度計算サイト 余弦定理 Geisya 今いろいろやって、二等辺三角形の辺の長さを求めるのをやってたら、 底辺以外の辺の長さをxとした場合、それぞれ頂角が30°,1°なら、底辺の長さが x(√2√6)/2, x√3になったんですけどあってますか?14 例題2辺の長さが分かっている直角三角形、もう1辺の長さを求めてみよう! 141 1問目;
学習指導法 のブログ記事一覧 2ページ目 マッキーのつれづれ日記
不等辺三角形 辺の長さ 中学
不等辺三角形 辺の長さ 中学-凸多角形の定義と認識方法 点列P=(p 0, p 1, p 2, , p n=p 0)が凸多角形を成すかどうかの判定: s ij 頂点p iとpjを結ぶ線分(対角線),ij≧2 仮定:多角形の辺は反時計回り(内部は辺の左)に順序付三角形と四角形の面積の求め方を覚えましょう。 三角形の面積=底辺×高さ÷2 ※ 「高さ」がどの部分の長さなのかをていねいに考えて下さい。 長方形の面積=たて×よこ 正方形の面積=1辺×1辺 平行四辺形の面積=底辺×高さ ひし形の面積=対角線×対角線÷2 台形の面積= (上底+下底)×高さ÷2 ※台形の面積は特に忘れやすいので注意が必要です。



このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋
フジテレビ金曜プレステージ 浅見光彦シリーズ49「不等辺三角形」 《放送日》 平成26年1月17日(金) 《原作》 内田康夫「不等辺三角形」徳間文庫刊 《脚本》 峯尾基三 《監督》 柿沼竹生 《出演》 中村俊介、榎木孝明、野際陽子不等辺三角形の選択した3つの入力値から他の要素の値を計算します。 入力指定 3辺abc 2辺abと高さ (Cは鋭角) 2辺abと高さ (Cは鈍角) 2辺bcと高さ (BとCが鋭角) 2辺bcと高さ (BかCが鈍角) 2辺abと夾角C 辺aと高さと角C 2角BCと夾辺a 2角BCと高さ 面積と2辺ab (Cは鋭角) 面積 3辺の長さが与えられたときの三角形の面積(中学・高校数学) とりあげた。 授業では、ヘロンの公式を用いる方法(解法2)と教科書にある余弦定理の応用として求める方法 (解法3)を扱った。 いたことを思い出した。 現在の中学数学で三平方の定理
A 2 16 − 16 = 25 − 16 {\displaystyle a^ {2}1616=2516} a 2 = 9 {\displaystyle a^ {2}=9} a = 3 {\displaystyle a=3} これで直角を成す2辺(aとb)の値を面積の公式に当てはめることができます: Area = 1 2 ( b h) {\displaystyle {\text {Area}}= {\frac {1} {2}} (bh)} Area = 1 2 ( 4) ( 3) {\displaystyle {\text {Area}}= {\frac {1} {2}} (4) (3)}正弦定理から,三角形の辺の長さを求める計算について ABCにおいてa = 3 ,A = 60°,B = 45°のときbを求めよ。 という問題がありますが, これを定理にあてはめていって, b = 3 / sin60°× sin45° まではつくれるんですが,そこから (3 ÷ √3/2 ) × 1/√2= 6/√6=√6 というのになるのが,意味がわかりまStep 1 で, b , A はわかりますが,もう1つの辺の長さ c はわかりません。そこで, c を求めるために,まずC = 180° A B より,C を求めます。 Step 2 Step 1で求めたCを用いて, つまり辺の長さ c を求めます。 これで,2辺 b , c とそのはさむ角 A がわかりました。あとは,公式に当てはめれ
21年5月28日(金) 10~1358 <bsフジサスペンス劇場>『浅見光彦シリーズ49 不等辺三角形』 21年5月28日(金) 10~1358この数値はs = (abc)/2 で求められます。 三辺の長さがa = 4、b = 3、c = 5の場合s = (435)/2となり、s = (12)/2からs = 6になります。 ヘロンの公式の次の段階、A (面積)=sqr {s (sa) (sb) (sc)}を使用します(注:sqrはルートを意味します)。 Aには三角形の面積の公式をあてはめます。 つまり、1/2bh、1/2ah、または1/2chのどれを代入しても問題ありません。 計算をしてhを求めます。直角三角形のときに利用できる 辺の長さの関係式でしたね。 それを発展させて考えていくと 直角三角形だけでなく 鋭角、鈍角三角形を見分ける方法として活用することができます。 入試などでは、活用する機会は少ないと思いますが




学習指導法 のブログ記事一覧 2ページ目 マッキーのつれづれ日記




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集
ですが当然、このように揃った三角形ばかりではありません。 「どの辺もそろってない」という三角形も存在します。 その名も「不等辺三角形(ふとうへんさんかっけい)」。 字の通り、どの辺も等しくない三角形ですね。三角形を作るための条件 三角形には、 2つの辺の長さを足し合わせると残りの1つの辺の長さより長くなる。 また、2の辺の長さを引いた時、残りの1つの辺の長さより短くなる。 という定理がある。この定理の詳細は三角形の2辺の和と差のページを参考にし三角形の面積(2辺と夾角から) 高精度計算サイト 辺の長さ a 辺の長さ b 2辺間の夾角 θ 度 ラジアン 面積 S 周囲の長さ L 高さ h \) お客様の声 アンケート投稿 よくある質問 リンク方法 三角形の面積(2辺と夾角から) 110 /11件 表示件数 1 2129 男 / 60歳以上使用目的




黄金三角形による18 シリーズの三角比 おいしい数学



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン
直角三角形の斜辺の長さを求める 3つの方法 wikiHow; 三平方の定理で直角三角形の辺の長さを計算してみると、 x² = 3² 5² x = √34 になるね。 答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。 Step3 ピタゴラスが悩んだ直角二等辺三角形 つぎは、 直角二等辺三角形の辺の長さ を三平方ので中学生でできなくても大丈夫です。 中学校では発展学習として掲載されている教科書があります。 (1) 右図のように 三辺の長さだけ が与えられた三角形で、「 高さAH 」や「 三角形の面積 」を求めるには BH=xとおいて (このときCH=6xとなります) AHの長さ (の2乗)を2とおりの方法で表わせば解けます。 (√13) 2 x 2 = AH 2 = 5 2 (6x) 2 (√13)2x2 = 52 (6x)2 13x 2 =25 (36




二等辺三角形の面積



ベストコレクション 不等辺三角形 高さ 求め方 不等辺三角形 高さ 求め方 小学生
直角三角形の合同条件 以下の 2 2 つを利用します。 1 斜辺と 1 1 つの鋭角がそれぞれ等しい。 この 2 2 つは暗記してください。 三角形の合同条件 3 3 つを暗記しましたね? 同じことです、覚えないと話になりません。三角不等式は様々な「長さ」に拡張されています。→いろいろな三角不等式(絶対値,複素数,ベクトル) 三本の不等式を a a a について解くことで,条件を ∣ b − c ∣ < a < b c bc余弦定理を変形すれば、 b , c , a が分かっているときに A を求めるという使い方もできます: a 2 =b 2 c 2 −2bc cos A この式をよく見ると、 「右辺は辺の長さだけ」 でできており、 左辺は角度だけ でできています。 したがって、この式を利用すると 「3辺の長さ」から、 「角 A 」 を求める ことができます。 (正確には、角 A そのものではなく cos A が求まりますが




三平方の定理の応用




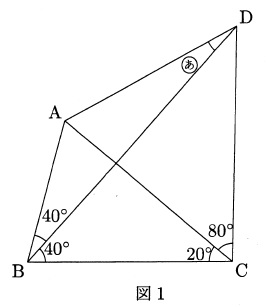
1 の問題で 自分の証明でも合ってますか 字が汚くてすいません Clear
アルミ製アングル(不等辺) アルミアングルmm×30mm~25mm×50mm アルマイトシルバー 長さ3m(アングル材・チャンネル材・バー材)の詳細です。ソニテックでは数量問わず現場に直接お届け。現場監督の仕入れの手間を大幅に減らせます。同じ直角三角 形を2個重ね るとき、重ね 方を変えると 重なった部分 の面積が変わ ることに気付 く。 <課題> 1辺10cmの正方形を対角線で2等分し、 直角二等辺三角形を2個作る。この2個の直 を原点に一致させ、辺FDをx軸上に重ね固 定する。Myersの記述では、三角形とならない場合に辺の長さ a = b、b = c、c = a との組み合わせが考慮されていません。そのため、三角形とならない場合の準正常ケースではテストケース数が6件となっていま



三角形の種類 中学から数学だいすき




解答 オリジナル問題2 2つの辺の長さが同じ三角形 図形問題で柔らか頭に 算数オリピック 中学入試問題にチャレンジ
計算すると、 4 9 = c × c 13 = c × c よって、長い辺の長さは c = 13 (二乗して 13 になる正の数)となります。 では、 13 はどれくらいの長さでしょうか? 3 × 3 = 9 c × c = 13 4 × 4 = 16 なので、 13 は 3 より大きくて 4 より小さい数だと分かります。不等辺三角形の選択した3つの入力値から他の要素の値を計算します。 入力指定 3辺abc 2辺abと高さ (Cは鋭角) 2辺abと高さ (Cは鈍角) 2辺bcと高さ (BとCが鋭角) 2辺bcと高さ (BかCが鈍角) 2辺abと夾角C 辺aと高さと角C 2角BCと夾辺a 2角BCと高さ 面積と2辺ab (Cは鋭角) 面積 まとめ:直角二等辺三角形の辺の長さの求め方は2通りでクリア! 直角二等辺三角形の辺の公式はシンプル。 斜辺を求めるとき → √2をかける 斜辺以外を求めるとき → √2/2をかける で計算できちゃうんだ。 ガンガン問題をといていこう! そんじゃ




黄金三角形による18 シリーズの三角比 おいしい数学



このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋
2 三平方の定理より、直角三角形かどうか判断できる! 21 例題ある3辺をもつ三角形は直角三角形かどうか中学生からの質問(数学) や が出てくるのは,次の2つの特別な直角三角形の場合です。 直角三角形においては三平方の定理が成り立つため,3つの角が30°,60°,90°である直角三角形と,45°,45°,90°である直角三角形の3辺の長さには,それぞれ次のような関係が成り立っています。 特別な直角三角形の3辺の比 30°,60°,90°の直角三角形の2 辺の長さがわかれば,残りの辺の長さは,三平方の定理を利用して求めるこ とができる。直角をはさむ2 辺の長さをa,bとし,斜辺の長さをcとすると ・a,bが与えられたとき cab=+22 ・b,cが与えられたとき acb=-22 三平方の定理の逆 三角形の3 辺の長さa,b,cの間に



三角形の公式 Wakatta




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
3辺が分かる三角形の面積 3辺の長さが4, 5, 6である三角形の面積を求めなさい。 今回は として, 余弦定理で の値を求めてから, にそれを代入し, の値を求めて面積の公式に当てはめて求めるという方針で 赤い線で示すように、三角形と平行四辺形に分けます。 三角形の三辺の長さは26、65、67となります。 ここでヘロンの公式を使って三角形の面積を出します。 S=√(s・(sa)・(sb)・(sc)) Sは求める面積、a、b、cは辺の長さです。sは下式です。 s=(1/2)×(abc)今分かっている情報は、 「1辺3角(c=6,A=60°,B=75°,C=45°)」 だよね。 1辺2角を使って他の辺の長さを求めるときには、 正弦定理 を突破口としよう。 aとbどちらから求めにいくのがいいかな? どちらも同じではないんだ。 aに対応する ∠Aは60° 、bに対応する ∠Bは75° だ。 sin60°なら計算できるけれど、sin75°の値は勉強していないよ。 というわけでここは、 ∠A と



11 7 数学 図形 これは 不等辺三角形 ふとうへんさんかっけい ですか 辺が揃ってない三角形の話 のっぽさんの勉強メモ



三角形 辺 の 長 さ 比率 238n424 Proxydns Com




高校数学 三角比による三角形の面積の公式 S 1 2bcsina の証明と利用 受験の月
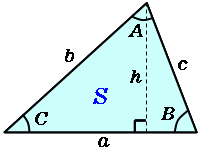



不等辺三角形 高精度計算サイト
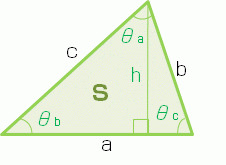



三角形の公式 Wakatta
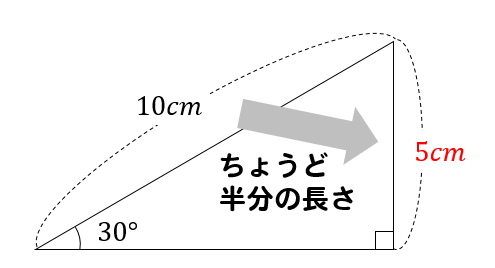



小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ
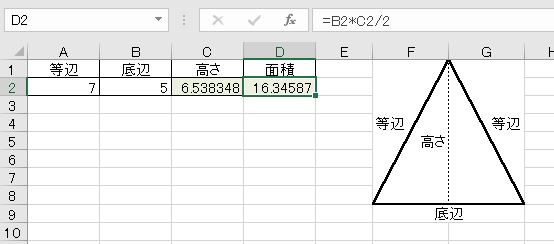



Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




小学6年生で三角形の面積求め方わかりません 小学6年生の親です 学 数学 教えて Goo
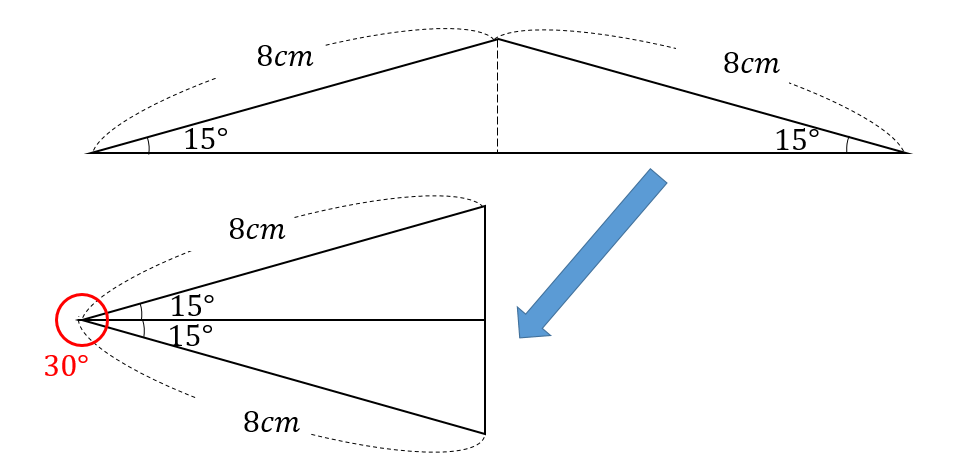



小学算数 15度 75度の三角形ってどうやって面積求める 数スタ
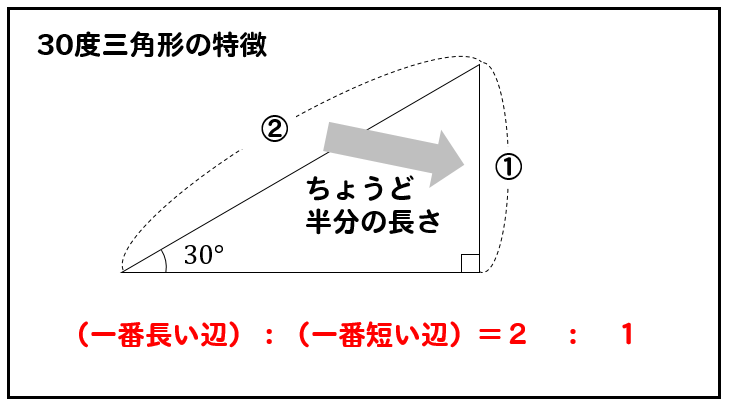



小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ




直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学
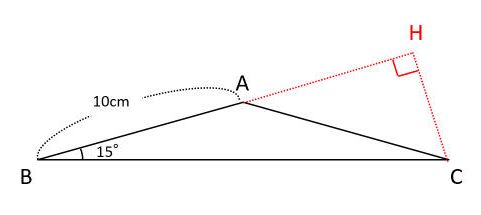



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学
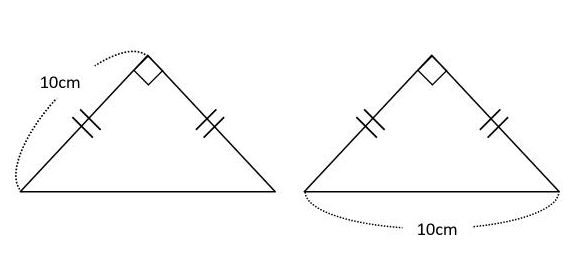



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




中学数学 裏技 三角形の角の二等分線の長さを求める下書き やはり俺の考察ブログはまちがっている アニメ 数学




中学数学 直角三角形の辺の長さの求め方 超丁寧に なぜか分かる はかせちゃんの怪しい研究室



このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



年度 早稲田中学過去問2回目 算数 大問4解説 家庭教師サボの部屋




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
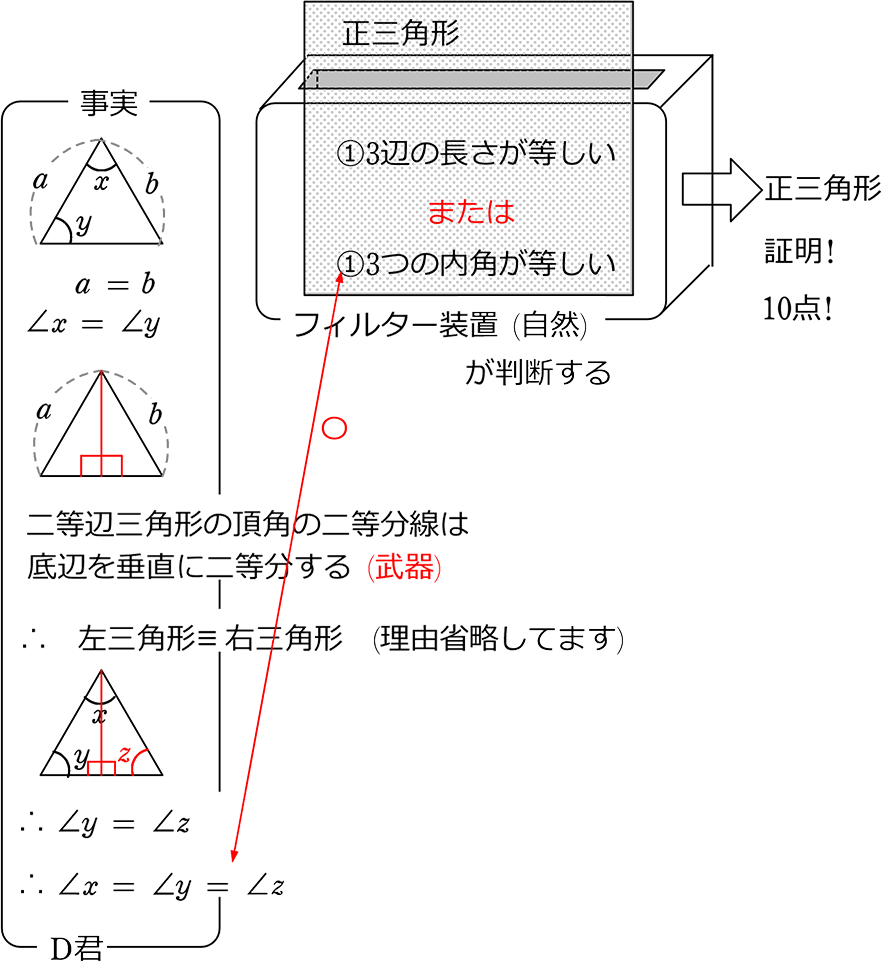



中学数学 図形の合同 図形の性質




中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



第18回 え マジっすか そんなの知らなかったテクニック Mysolidworks
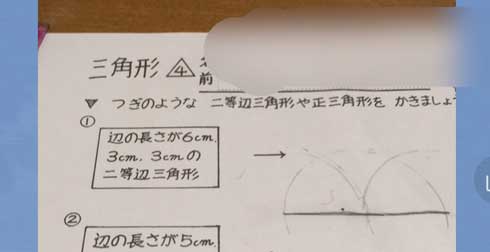



娘の算数の宿題が鬼畜難易度 これは難問 俺も解けない 非ユークリッド幾何学教えてるのか ねとらぼ




数学 中2 64 二等辺三角形 Youtube
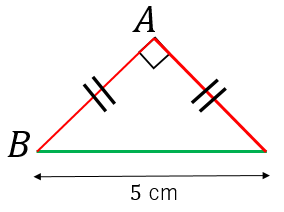



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




直角三角形の辺を求める Youtube




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく
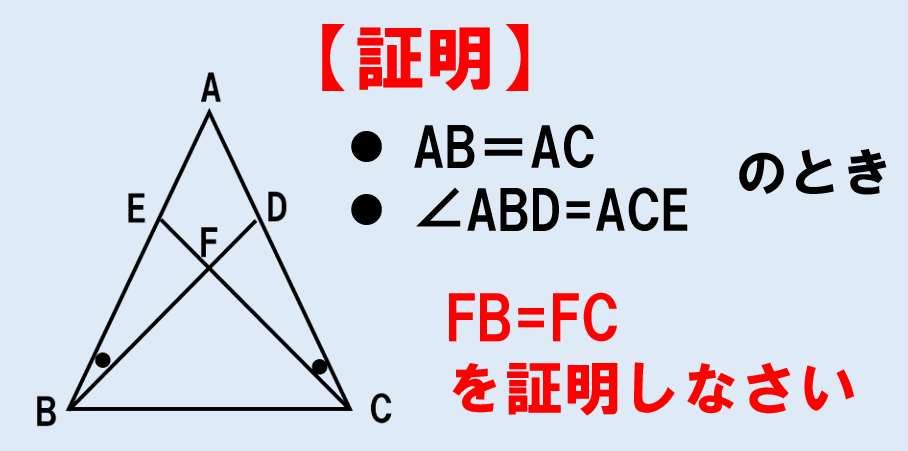



中2数学 2角が等しい三角形 二等辺三角形の長さを用いた証明 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく




不等辺三角形 至急ご回答お待ちしております 不等辺三角形について その他 学校 勉強 教えて Goo




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



辺の長さに注目する 中学受験 田中貴 Com
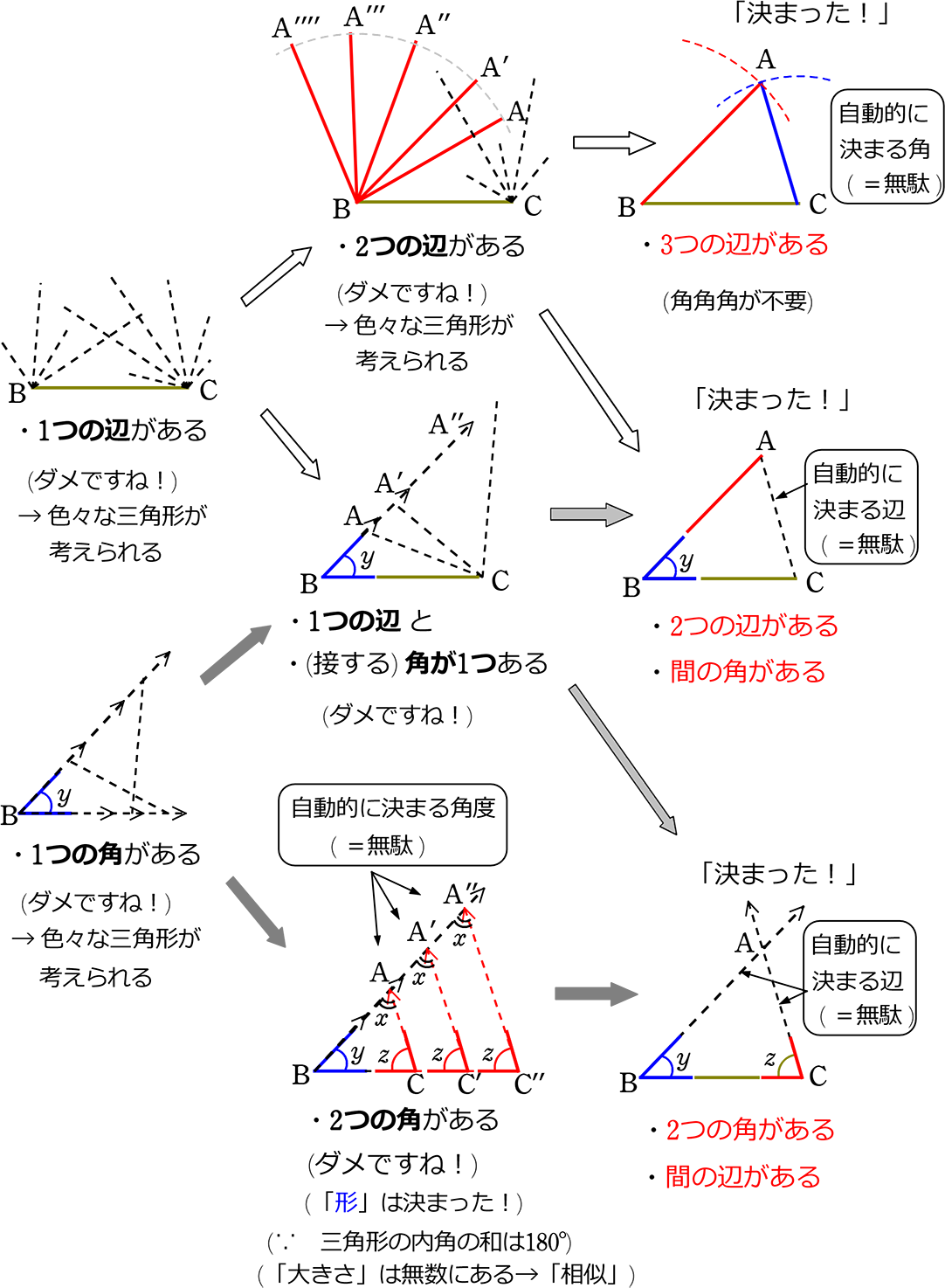



中学数学 図形の合同 図形の性質




三角比 30 45 60 もう一度やり直しの算数 数学



3
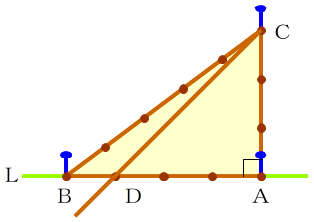



3 4 5の三角形で 本当に直角ができる Note Board
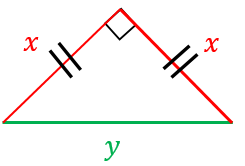



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学



第18回 え マジっすか そんなの知らなかったテクニック Mysolidworks
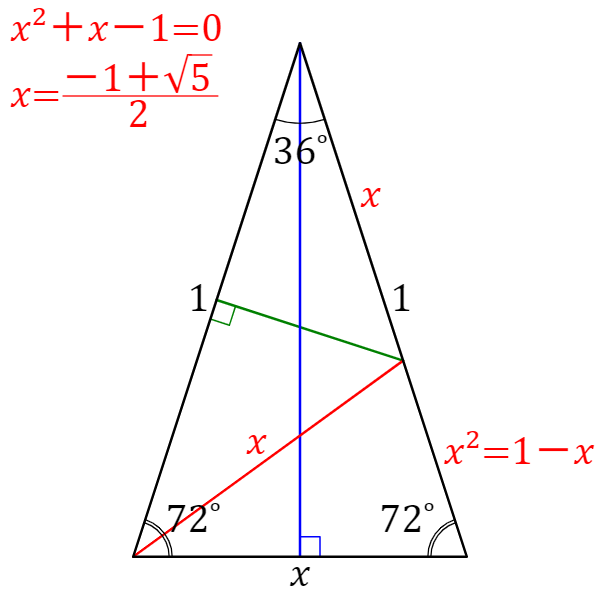



Sin18 Cos72 Cos36 Sin54 を簡単に求める方法 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog
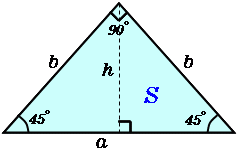



直角二等辺三角形 高精度計算サイト



このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋



正三角形 二等辺三角形 直角三角形の書き方 作図 まとめ 受験辞典




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導
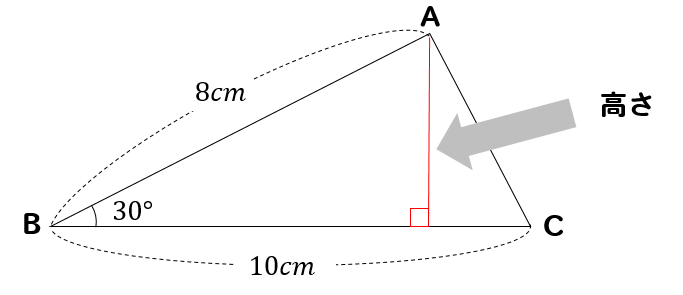



小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ
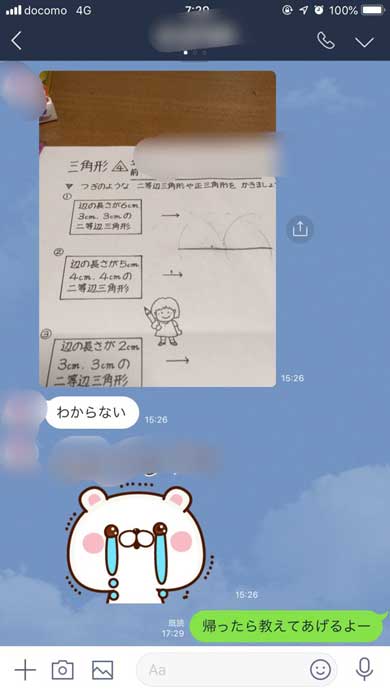



娘の算数の宿題が鬼畜難易度 これは難問 俺も解けない 非ユークリッド幾何学教えてるのか ねとらぼ




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
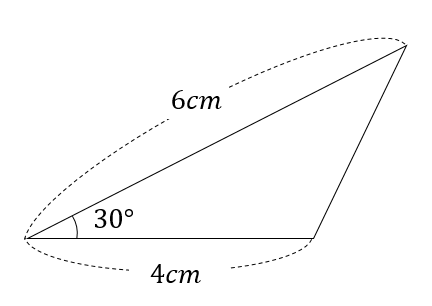



小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




二等辺三角形の底角は本当に等しいのか ひと筋縄ではいかない証明 ブルーバックス編集部 ブルーバックス 講談社 1 4
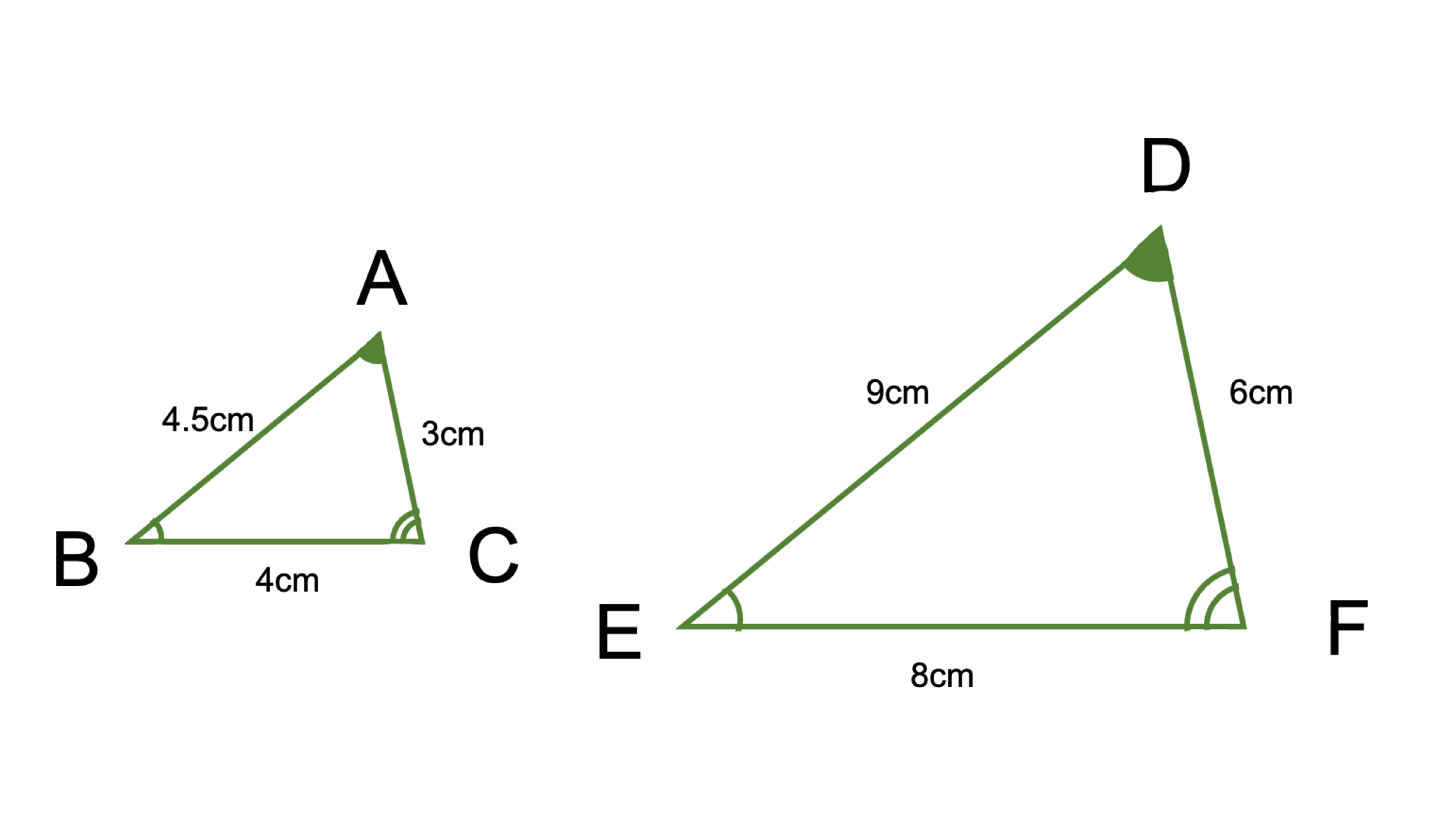



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



辺の長さに注目する 中学受験 田中貴 Com



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学



不等辺三角形の高さについてです 画像のa B C 角a Yahoo 知恵袋




数学 中2 64 二等辺三角形 Youtube




簡単公式 二等辺三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




黄金三角形による18 シリーズの三角比 おいしい数学



Q Tbn And9gcswvrt8ha48xdbfrcblwxj6unke6elnukctrjl1ijr8agfa8v Usqp Cau
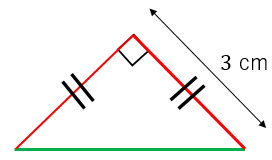



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学



3




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく



正三角形 二等辺三角形 直角三角形の書き方 作図 まとめ 受験辞典




中学数学 直角三角形の辺の長さの求め方 超丁寧に なぜか分かる はかせちゃんの怪しい研究室




数学 中3 61 三平方の定理 基本編 Youtube




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学



中学から数学だいすき




高校1年生数学の問題です 1 直角を挟む2辺の長さの和が16である直角 中学校受験 教えて Goo




任意の三角形は二等辺三角形である Fukusukeの数学めも




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



Www Kyoiku Shuppan Co Jp Tsushin Files 17st 04sugaku Pdf



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
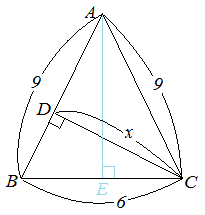



三平方の定理の応用



1




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比
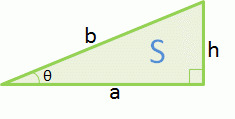



三角形の公式 Wakatta




三角定規 授業がんばりmath




中学入試算数 全2問 工夫したらひらめく良問 暇つぶしに動画で脳トレ



正三角形 二等辺三角形 直角三角形の書き方 作図 まとめ 受験辞典




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比




3 4 5の三角形で 本当に直角ができる Note Board



No comments:
Post a Comment